参考:
- https://zhuanlan.zhihu.com/p/36581276
- https://blog.csdn.net/m0_57980287/article/details/117675703
gamma的由来
Gamma 的由来,说法是不统一的。
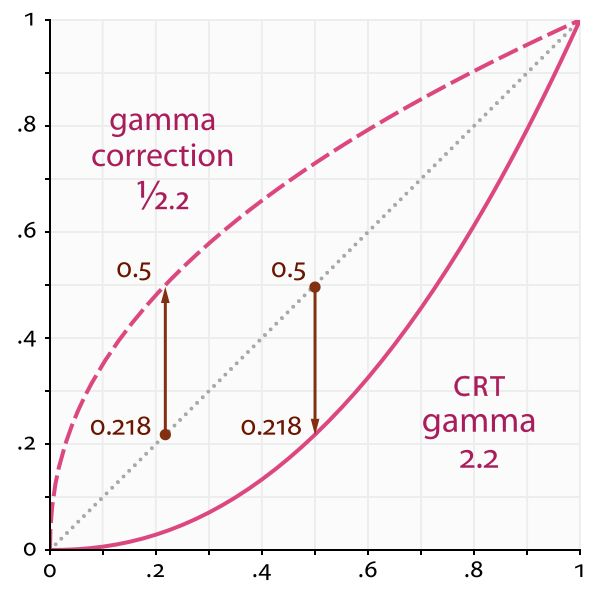
部分人认为是由于早期 CRT 显示器的问题,即输出的亮度和输入的电压并非线性关系,而是近似 2.2 次幂的关系,导致进入人眼的亮度要比计算机上存储的亮度要低。例如,计算机上存储的亮度为 0.5,经过显示器调整后变为 0.5 的 2.2 次幂,即 0.218。为了让进入人眼的亮度与计算机中存储的值相同,需要在显示器调整前将亮度变为自身的 1/2.2 次幂,即 0.73,这样在经过显示器的调整,进入人眼就是 0.5 了,也就是说,Gamma 校正可以补偿由于显示器造成的亮度下降。这里需要注意的是,2.2 这个值是一个近似值,或者可以说是一个标准,实际上可能会有不同,现在的显示器甚至可以调节。
还有一种说法是,人眼对不同亮度的敏感程度是不同的,对暗部的敏感要高于亮部(这个是没错的)。而存储颜色的空间是有限的,例如常用的 RGBA32 格式,每个颜色通道都只有 8 位,只能存储 256 种亮度,所以基于人眼感知的原因,用更多的空间存储更多暗部的颜色是更合理的。人眼感知到的中间亮度值大概是 0.18,换算到 0.5 大约是 pow(0.18, 0.4042),也就是说大约可以用 0.4042 这个指数(但是也有说通过人为测量,指数定到 0.45 的,这里不必纠结,因为本身就是近似值,每个人感知的也不一样),来计算亮度最终变换后的结果,以存储更多暗部的亮度值(后面会详细讲解为什么这么做可以存储更多暗部的亮度值)。当然显示的时候,依然需要把这个亮度再变换到幂运算之前的结果,以显然原本的颜色,不过实际上并不需要这么做,因为这里有一个美妙的巧合,那就是我们用来提高暗部存储范围的指数,恰好和测量出的显示器调整输出亮度的指数近似为倒数,也就是说,什么也不用做,显示出来的自然就是原本的颜色。
举例\
通常情况下,设计师制作好的图片一般都是基于自己观察到的,也就是基于物理世界的亮度值,因为有显示器调节降低亮度的缘故,实际上在计算机中存储的是观察到的亮度值的 0.45 次幂(以下 Gamma 值都算作 2.2, 1 / 2.2 约等于 0.45),因为物理世界是线性空间的,所以这种情况下计算机中存储的值就是 sRGB 空间。如果用 sRGB 空间的值计算光照,则光照算法实际上是有些问题的。
举个例子,设计师制作了一张亮度值为 0.5 的图(0.5 指的是计算机中存储的原图亮度,也就是 sRGB 空间),经过显示器调解后,亮度变为 0.218。这时如果使用名为“将亮度变为原来的 2 倍”的算法时,如果直接将计算机中的 0.5 乘上 2 ,即为 1,再经过显示器调解,输出出来的亮度值还是 1 (因为是 1 的 2.2 次幂)。从 0.218 到 1,亮度变为之前的 4 倍多,这并不是我们预期的(注意我并没有说这样的效果一定不好,只能说不是我们预期的)。所以我们需要先把计算机中的亮度值还原成线性空间的,也就是将 0.5 变换为线性空间的值 0.218,再乘 2 变为 0.436,此时依然是线性空间中。不过这时候不能直接输出,因为显示器会把 sRGB 的值变换到线性空间,如果计算机中存储的是线性空间的值,那么把线性空间的值再进行一次变换,就是错误的,所以我们需要再把 0.436 这个线性空间的值再重新变换到 sRGB 空间,即 pow(0.436, 0.45) 约等于 0.688,最后再经过显示器的调解后,变为 pow(0.688, 2.2) 约等于 0.439,这样观察到的物理世界亮度基本就是原来的 2 倍了(原来的物理世界中的亮度为 0.218)。
为什么需要gamma矫正
先看看颜色的来源
线性空间中的颜色 如果程序中获取到的颜色值是基于线性的,比如说手动输入了一些颜色值,那么想把这些颜色理想的显示出来,就要对他们进行Gamma校正,这样才能保证显示器在显示出来后是原来的颜色
非线性空间中的颜色 非线性的颜色指的是执行过Gamma分之一次方后的颜色,也就是已经执行过Gamma校正的颜色,如果程序获取到的是这种颜色,就不需要再进行Gamma校正,直接发送给显示器显示即可
非线性空间中的颜色从何而来? 这是一个非常简单,但又非常值得细品的一个问题:
当你在电脑上绘制完一张理想的图片后,请你再回想一下给图片设置颜色的过程;无论在任何时候,你设置的颜色都是根据你在显示器前看到的颜色,这就意味着所有创作出来的图片的颜色都是被显示器执行过Gamma次方后的颜色,而这都是你理想中的颜色,那么你给图片所设置的颜色,不恰好正是最终显示出来颜色值的Gamma分之一次方?所以你在无意识中就做出了一张经过Gamma校正过的图片,而且可以肯定的是,几乎所有图片中的颜色都是经过Gamma校正过的
再总结一下:非线性空间中的颜色指的是经过Gamma校正的颜色,就是从创作出来的图片中读取的颜色,他们在一般情况下可以直接发送给显示器直接显示
那么问题来了:二班情况是什么? 其实“一般情况”指的是:不需要对颜色值进行再次加工,比如说光照计算、混合等一些操作;那么“二班情况”当然就是要对颜色值进行再次加工了;比如说,当有两张图片需要混合时,就要先对他们各自进行Gamma次方计算,变换到线性空间中(变换成理想的颜色值),再进行混合,混合完之后再进行Gamma校正,最后发送给显示器显示
那么问题又来了:二班的情况为什么要变换到线性空间中? 这个问题最后回答
还有一个问题:上面说“几乎”所有图片中的颜色都是经过Gamma校正过的,那么有什么图片不是?举个栗子:在基于物理的渲染中(PBR),为了高效的实现光照,常常会用到漫反射贴图、镜面光照贴图和法线贴图等一系列贴图,这里的镜面光照贴图和法线贴图通常都不是,他们用的是线性空间中的颜色
最后再再总结一下: 如果用线性空间中的颜色发送给显示器显示,在显示之前要进行Gamma校正;如果用非线性空间中的颜色,则可以直接发送给显示器显示;但是,如果要对非线性空间中颜色的图片进行加工,就要在加工前先进行Gamma次方计算,加工后再进行Gamma校正,之后才能发送给显示器显示
gamma矫正转换公式
sRGB to CIE XYZ:
$$
sRGB(x) = \begin{cases} 12.92 x, &x\lt= 0.0031308 \[2ex] 1.055 x ^ {1/2.4} - 0.055, &x\gt 0.0031308 \end{cases}
$$
$x$为线性空间中的颜色。
CIE XYZ to sRGB:
$$
linear(x) = \begin{cases} \frac {x} {12.9}, &x\lt= 0.04045 \[2ex] (\frac{x + 0.055} {1.055}) ^ {2.4}, &x\gt 0.04045 \end{cases}\[2ex]
$$
$x$为sRGB空间中的颜色。
rec.2020 to CIE XYZ:
CIE XYZ to rec.2020

